Sünme Nedir? Betonda Sünme Şekil Değiştirmesi
İçerik
Sünme, betonda büzülmeye ek olarak, kalıcı yük altında zaman içinde oluşan deformasyon olarak tanımlanabilir. Kalıcı yükler altında betonda oluşan gerilmelerin basınç dayanımının %40’ından az olduğu durumlarda sünmenin gerilme ile orantılı olarak arttığı, gerilmenin daha fazla olduğu durumlarda ise bu orantının kaybolduğu ve sünmenin daha hızlı arttığı bilinmektedir.
Sünme ancak basınç gerilmeleri oluşturan kalıcı yükler altında meydana gelir. (Beton Basınç Dayanımları ve Dayanımları Etkileyen Faktörler) Eğer iki özdeş numuneden birisi yüklenmeden, diğeri kalıcı bir yük altında saklanır ve bu numunelerde belli bir zaman süresi içinde oluşan birim kısalmalar ölçülürse, sünme deformasyonu yüklenmiş numune deformasyonundan yüklenmemiş numunenin deformasyonu çıkarılarak hesaplanabilir. [1]
1. Sünme Bileşenleri
Sünme davranışının fiziksel olarak daha iyi anlaşılabilmesi için sünme şekil değiştirmesi birçok bileşene ayrılarak incelenebilir.
Elastik ve plastik sünme bileşenleri aşağıdaki şekilde gösterilmiştir.
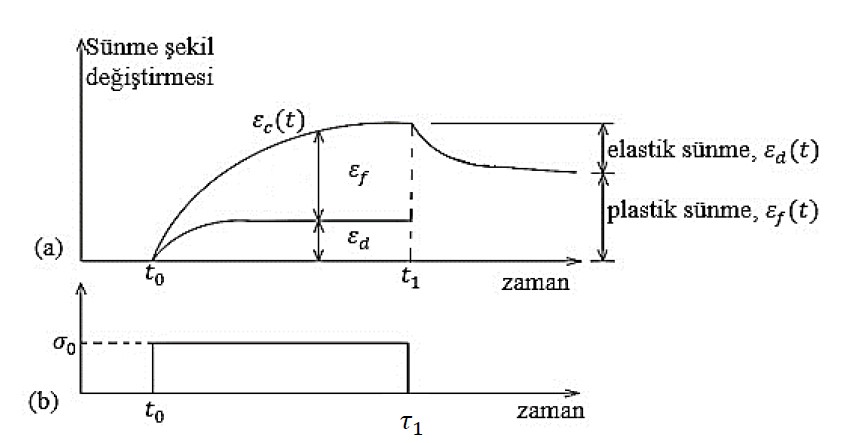
Sürekli olarak uygulanan σ0 gerilmesi etkisiyle sünme azalan bir şekilde artmaktadır. Gerilme t1 anında kaldırıldığında, sünme şekil değiştirmesinde ani bir değişimden ziyade zamanla gözlenen yavaş bir azalma gözlemlenir. Sünme şekil değiştirmesinin büyük bir kısmı plastik karakterdeyken bir kısmı elastik karakterdedir.
Sünme şekil değiştirmesinin geçici olarak kabul edilen elastik kısmı gecikmiş elastik şekil değiştirme olarak adlandırılmaktadır ve εd(t) ile gösterilmektedir. Uzun süreden beri yüklü tutulan bir beton numunesinden yük kaldırılırsa ortaya çıkacak gecikmiş elastik şekil değiştirme toplam elastik şekil değiştirmenin %50’sini oluştururken toplam sünme şekil değiştirmesinin %10 ila %30’una denk gelmektedir. Her ne kadar yük kaldırıldıktan sonra gözlemlense de yük altında geçen süre boyunca da aynı büyüklüğe sahip olduğu ve yüklemeden hemen sonraki zaman aralığında hızlı bir şekilde arttığı düşünülmektedir bu durum gecikmiş elastik şekil değiştirmesi için geçerlidir. Rüsch’e göre gecikmiş elastik şekil değiştirme eğrisinin şekli numune yaşından, boyutlarından ve beton karışımından bağımsızdır [2].
Büyük bir kısmı plastik karakterde olan sünme şekil değiştirmesi, yayılma olarak tanımlanır ve εf(t) ile gösterilmektedir. Bundan dolayı herhangi bir t andaki sünme şekil değiştirmesi aşağıdaki denklem ile gösterilir.
εc(t) = εd(t)+ εf(t)
Sünmenin yayılma bileşenini alt gruplara ayırmak için yüklemeden sonraki ilk 24 saatte görülen hızlı ilk yayılma olarak tanımlanmıştır ve εfi(t) ile gösterilmiştir. Hızlı ilk yayılma kalıcı şekil değiştirmeler doğmasına sebep olurken büyük ölçüde ilk yükleme anındaki beton yaşına bağlı olmaktadır. εfi(t) değeri o kadar büyük olur eğer numune ne kadar erken yüklenirse. Yüklemeden bir gün sonra görülmeye başlanan ve yavaş bir şekilde gelişen yayılma şekil değiştirme bileşeni ortamın bağıl nemine bağlı olup kendi içerisinde basit yayılma bileşeni, εfb(t) ve kuruma yayılma
bileşeni εfd(t) olmak üzere ikiye ayrılmaktadır. Kuruma yayılması, kuruyan bir ortamda yüklü olan numunede görülmesi mümkün kalıcı sünme şekil değiştirmesidir.
εc(t) = εd(t)+ εfi(t)+εfb(t)+εfd(t)
Sünme bileşenleri aşağıdaki şekilde gösterilmiştir.

εfb(t) Basit yayılma bileşeni, beton dayanımına, agrega türüne, miktarına, büyüklüğüne ve yükleme anındaki beton yaşına bağlıdır. εfd(t) Kuruma yayılma bileşeni ise numune şekli, boyutlarına ve nem miktarına bağlıdır. Beton Neden Çatlar? Beton Çatlakları – Çatlak Çeşitleri)
2. Yaş Etkisi
Sünme şekil değiştirmesinin bileşenleri, ilk yükleme anında betonun yaşında olduğu gibi bir dereceye kadar hidratasyon derecesinden etkilenirler. Bu bileşenlerden en çok etkilenenler, hızlı ilk yayılma εfi ve basit yayılma εfb‘dir.
Aynı özelliklere sahip fakat t0, t1 ve t2 gibi farklı zamanlarda yüklenen numunelerde gözlenen sünme davranışının zamana bağlı değişimi aşağıdaki şekilde gösterilmiştir.

εc∗(), t0, t1 ve t2 farklı zamanlarda meydana gelen sünme şekil değiştirmesidir. İlk olarak t anında uygulanan ve uygulanmasına devam edilen bir yük etkisiyle t anında ölçülen sünme şekil değiştirmesi εc(t,τ) ile gösterilmektedir. Yaş etkisi, zamanla birlikte değişen gerilme geçmişi altında sünme şekil değiştirmelerinin tahmin edilmesini zorlaştıran bir etmendir.
3. Sünme Katsayısı
Devamlı olarak sabit gerilme altında tutulan bir numunenin herhangi bir t anındaki sünme şekil değiştirmesinin ani şekil değiştirmesine oranı sünme katsayısı olarak tanımlanır ve Φ(t,τ) olarak gösterilmiştir.
Sünme katsayısının büyüklüğü ilk yükleme anındaki beton yaşına bağlı olduğu gibi sünme şekil değiştirmesinin ilk yükleme anındaki de buna bağlıdır.
Sünme ve ani şekil değiştirme bileşenleri gerilmeyle orantılı olduğundan Φ(t,τ) sadece zamana bağlı bir fonksiyondur ve uygulanan gerilmeden bağımsızdır. Φ*(t,τ) ile gösterilen zaman sonsuza yaklaştıkça sünme katsayısı da belirli bir son değere ulaşır ve bu da son sünme katsayısı olarak tanımlanmaktadır. Bu ulaşılan son değer betonun sünme kapasitesinin ifade edilmesinde kullanılan bir büyüklüktür. Sünme katsayısının da bilindiği düşünülerek herhangi bir t anında hızlı bir şekilde sünme şekil değiştirmesine ulaşmak mümkündür bu da denklemaşağıdaki yardımıyla gösterilmiştir.
Φ(t,τ)=εc(t,τ) /ε0(τ)
Burada Φ(t,τ), sünme katsayısına gösterirken, εc(t,τ), sünme şekil değiştirmesi ve ε0(τ) ani şekil değiştirmesine göstermektedir.
4. Süperpozisyon Prensibi
Süperpozisyon prensibi, betonarmedeki yüke bağlı olan şekil değiştirmeler gerilmeyle benzer olduğundan zamanla değişen gerilme altındaki yer değiştirmeleri tahmin edebilmek amacıyla süperpozisyon prensibinden yararlanmaktadır. İlk olarak McHenry tarafından süperpozisyon prensibinin betonarme uygulanması yapılmış olup bu prensip, τ1 anında uygulanan bir gerilme artımının etkisiyle ortaya çıkan şekil değiştirmenin diğer zamanlarda uygulanan gerilmelerden bağımsız olduğu düşüncesine dayanmaktadır. [3]
Kaynaklar; [1] Uğur ERSOY, Güney ÖZCEBE, Erdem CANBAY-Betonarme Davranış ve Hesap İlkeleri[2] ACI 435R – 95 (1995). Control of Deflections in Concrete Structures. ACI Committee 435: American Concrete Institute. [3] Gilbert, R. (1988). Time effects in concrete structures. Amsterdam: Elsevier Science publishers B.V. [4] Amanullah ZAMANİ-BETONARME YÜKSEK BİR BİNANIN ZAMANA BAĞLI DAVRANIŞININ İNCELENMESİ





