Gerilme Şekil Değiştirme İlişkisi
Gerilme, bir yapının kesitine dolayısıyla malzemesinin üzerine uygulanan basınç ve çekmenin bir ölçüsüdür ve statik denge kurallarıyla elde edilmektedir. Şekil değiştirmeler ise bir cisimdeki uzama ve kısalmaların ölçüsü ve büyüklüğü olup, kinematik büyüklük olarak anılmaktadır.
1605-1703 yıllarında yaşayan Robert Hooke’un gözlemlerine göre bir cisimdeki deformasyonlar onun üzerine uygulanan kuvvet veya yükler ile doğru orantılıdır. Dolayısı ile gerilme ve şekil değiştirme büyüklükleri birbiri ile bağlantılıdır. Bu bağıntı ise gerilme şekil değiştirme ilişkisi olarak bilinir.
Gerilme şekil değiştirme ilişkisinin tespiti için yapılan deneysel çalışmalar ise basınç ya da çekme deneyidir. Geleneksel olarak, sünek malzemeler üzerinde çekme deneyi, gevrek malzemeler üzerinde ise basınç deneyi yöntemi ile gerilme ve şekil değiştirme ilişkisi tespit edilir. İnşaat mühendisliği alanında çok kullanılan malzemeler olan çelik ve betonun da gerilme ve şekil değiştirme ilişkisi laboratuarlarda yürütülen deneyler ile bulunur. Çelik malzeme üzerinde çekme deneyi, beton malzeme üzerinde ise basınç deneyi yürütülerek gerilme şekil değiştirme ilişkisi tespit edilir. Aşağıda, çelik ve beton malzemeler için elde edilen tipik gerilme ve şekil değiştirme ilişkilerine ait grafikler verilmektedir.
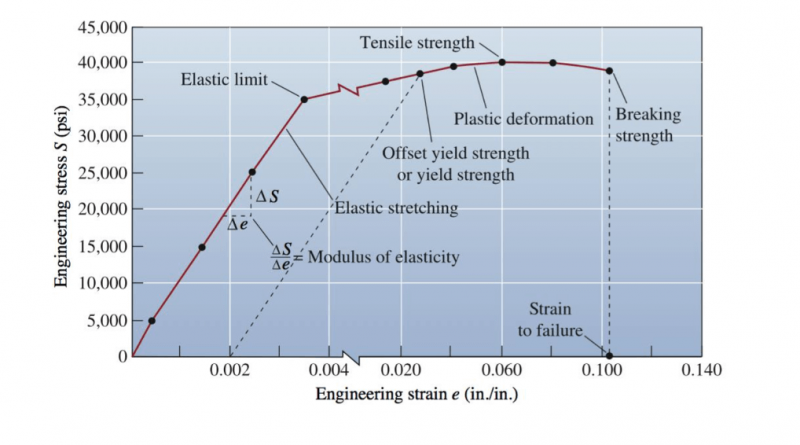
Çeliğin Gerilme Şekil Değiştirme İlişkisi

Doğrusal artış gösteren ilk bölüm çeliğin elastik bölge tanımını göstermektedir. Burada Hooke Kanunları geçerlidir. Grafiğin ilk bölümü içerisinde kalan kısım elastik şekil değiştirmeyi gösterdiği için yük etkisi kaldırıldığında malzeme önceki şekline geri dönecektir. Bu bölgede doğrunun eğiminden malzemenin Elastisite modülünü (E) bulmak mümkündür. Bu bölgenin en üst değeri çeliğin elastik limitini göstermektedir. Bu noktadan sonra oluşan sınır değeri elastisite sınır gerilmesi ismini almaktadır. Elastik bölgeden sonraki bölümde malzemede gerilme artışı yoktur ancak malzemedeki deformasyon yüksek hızla artar ve akma başlar. Bu bölge akma bölgesi olarak adlandırılır. Bu bölgede tasarım yapılırken kullanılan önemli faktörlerden biri olan ve akmaya yakın en az gerilme bilgisinin bulunduğu σy değeri okunmaktadır. Bu bölümden sonra kesit aksa da birim yoğunluk artış gösterdiğinden sertleşir ve dayanım bir süre daha devam eder. Bu bölge de Pekleşme bölgesi olarak adlandırılır. Bu bölgenin sonunda malzeme elastik bir davranış göstermeden en fazla dayanım altındaki oluşan maksimum gerilme değerine ulaşır. Bu (ultimate stress) σu olarak adlandırılır. Bu durumdan sonra malzemede sürekli olarak gerilme düşer ve şekil değiştirme miktarı artar. Deformasyonlar gözlemlenmeye başlar. Bu deformasyonların sonunda kopma noktası olarak isimlendirilen bölümde σf (kopma gerilmesi) değeri karşımıza çıkar.
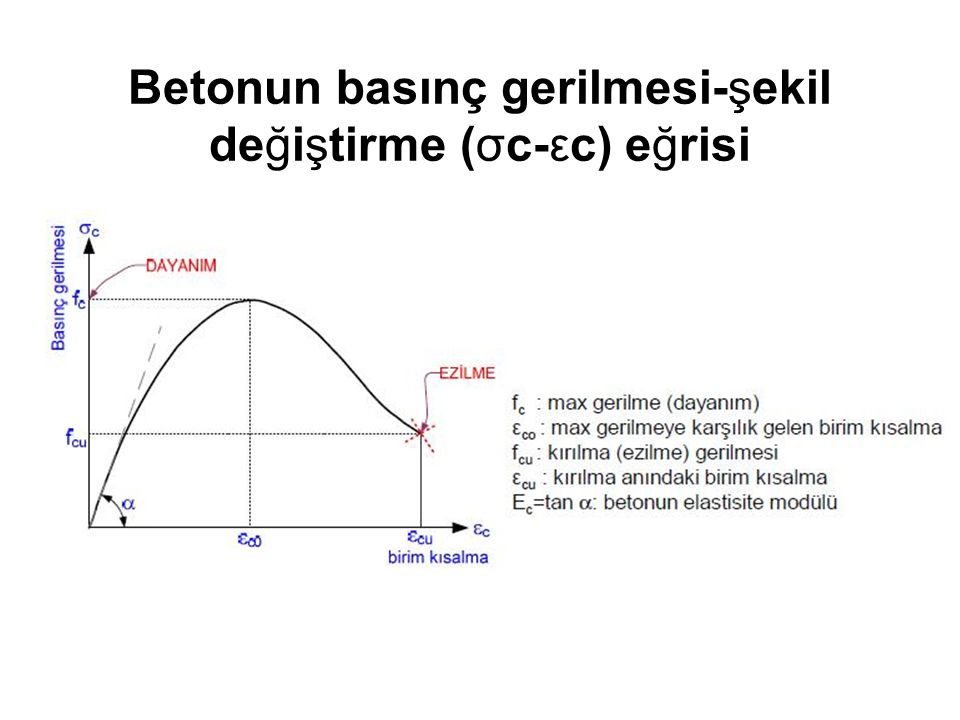
Yukarıda verilen gerilme şekil değiştirme eğrileri incelendiğinde, malzemelerin belirli bir gerilmeye kadar orantılı bir şekilde uzadığı, daha sonra ise gerilmedeki küçük değişimler sonucunda şekil değiştirmelerin daha fazla olduğu görülmektedir. Aradaki artış oranı ise doğrusal olmayıp eğrisel olmaktadır. Gerilme ve şekil değiştirmenin doğrusal orantılı olduğu bölgeye elastik bölge denilmektedir. Gerilme ve şekil değiştirmenin doğru orantılı olduğu bölgede cismin, Hooke cismi olduğu kabul edilerek, aradaki ilişkinin ise aşağıdaki gibi olduğu varsayılır.
σ=E ε
Diğer yandan cisimler üzerinde oluşan boy değişimi ve şekil değiştirmeler sadece cisim üzerine etkiyen yük ve kuvvetler tarafından oluşturulmazlar. Sıcaklık değişimleri de boy değişimi ve şekil değiştirmelere sebep olurlar. Ortaya çıkan şekil değiştirme sıcaklık değişimiyle doğru orantılıdır. Cismin tüm bünyesinde sıcaklık değişimi düzgün olduğunda, birim uzamanın ifadesi şu şekildedir:
εt=α Δt
Burada birim uzama, sıcaklık nedeniyle oluşan şekil değiştirmesi, ΔT, Sıcaklık değişimi, α ise bu iki büyüklüğü birbirine bağlayan malzemeye ait olan bir katsayı olup, sıcaklık genleşme katsayısı olarak bilinmektedir.
Böylece, cisim üzerinde oluşan toplam şekil değiştirme hem sıcaklık hem de gerilmelerden dolayı şu şekilde olur:
ε= σ/E+α Δt